BASIC CONCEPTS AND CONVENTIONAL METHODS OF STRUCTURAL

BASIC CONCEPTS AND CONVENTIONAL METHODS OF STRUCTURAL

ANALYSIS

1 INTRODUCTION

The structural analysis is a mathematical algorithm process by which the response of a
structure to specified loads and actions is determined. This response is measured by
determining the internal forces or stress resultants and displacements or deformations
throughout the structure.
The structural analysis is based on engineering mechanics, mechanics of solids,
laboratory research, model and prototype testing, experience and engineering judgment.
The basic methods of structural analysis are flexibility and stiffness methods. The
flexibility method is also called force method and compatibility method. The stiffness
method is also called displacement method and equilibrium method. These methods are
applicable to all type of structures; however, here only skeletal systems or framed
structures will be discussed. The examples of such structures are beams, arches, cables,
plane trusses, space trusses, plane frames, plane grids and space frames.
The skeletal structure is one whose members can be represented by lines possessing
certain rigidity properties. These one dimensional members are also called bar members
because their cross sectional dimensions are small in comparison to their lengths. The
skeletal structures may be determinate or indeterminate.

2 CLASSIFICATIONS OF SKELETAL OR FRAMED STRUCTURES

They are classified as under.

1) Direct force structures such as pin jointed plane frames and ball jointed space
frames which are loaded and supported at the nodes. Only one internal force or
stress resultant that is axial force may arise. Loads can be applied directly on the
members also but they are replaced by equivalent nodal loads. In the loaded
members additional internal forces such as bending moments, axial forces and
shears are produced.
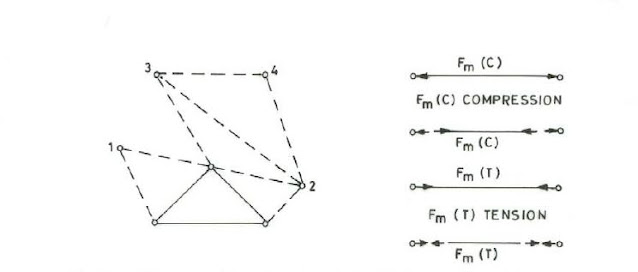
The plane truss is formed by taking basic triangle comprising of three members and three
pin joints and then adding two members and a pin node as shown in Figure 2.1. Sign 

Fig:-2.1 formation of plan triangulated truss and sign convention for internal member forces

Fig:- 2.2 Pin Jointed Plane truss subjected to member and nodal lodal loads

Fig:- 2.4 Ball and socket(Universal) jointed space Truss with nodal loading.

Fig:-2.3 Equlivalent nodal loads and free body of loaded member as beam

Fig:-2.4 Ball and socket(Universal) jointed space Truss with nodal loading

Fig:-2.5 Plane Frame Subjected to in plane external loading   Fig:-2.6 Internal Forces developed at                                                                                                            section a due to applied loading

Fig:-2.7 Plane grid subjected to normal to plane loading

Fig:-2.8 Internal stress resltants developed in members at A and B due to applied loading 

Fig:-2.9 Space frame subjected to general external loading

Fig:-2.10 Internal Forces Generated at A and B and reactions developed at c due to external loading

Convention for internal axial force is also shown. In Fig.2.2, a plane triangulated truss

with joint and member loading is shown. The replacement of member loading by joint

loading is shown in Fig.2.3. Internal forces developed in members are also shown.

The space truss is formed by taking basic prism comprising of six members and four ball

joints and then adding three members and a node as shown in Fig.2.4.

2) Plane frames in which all the members and applied forces lie in same plane as

shown in Fig.2.5. The joints between members are generally rigid. The stress

resultants are axial force, bending moment and corresponding shear force as shown

in Fig.2.6.

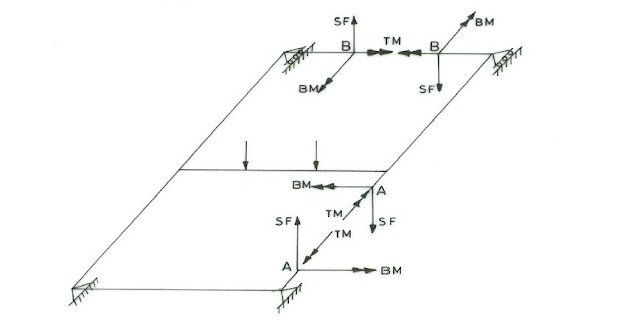
3) Plane frames in which all the members lay in the same plane and all the applied

loads act normal to the plane of frame as shown in Fig.2.7. The internal stress

resultants at a point of the structure are bending moment, corresponding shear force

and torsion moment as shown in Fig.2.8.

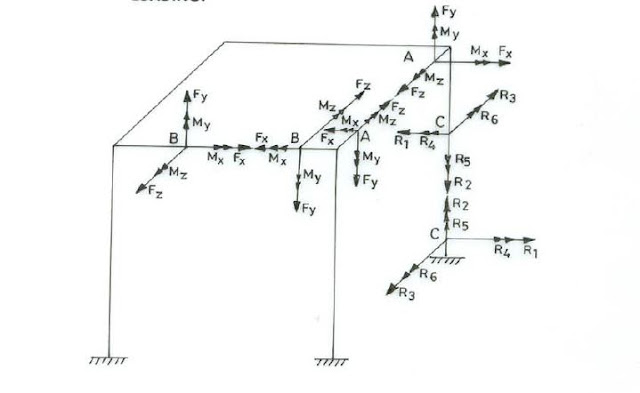
4) Space frames where no limitations are imposed on the geometry or loading in

which maximum of six stress resultants may occur at any point of structure namely

three mutually perpendicular moments of which two are bending moments and one

torsion moment and three mutually perpendicular forces of which two are shear

forces and one axial force as shown in figures 2.9 and 2.10.

3 INTERNAL LOADS DEVELOPED IN STRUCTURAL MEMBERS

External forces including moments acting on a structure produce at any section along a

structural member certain internal forces including moments which are called stress

resultants because they are due to internal stresses developed in the material of member.

The maximum number of stress resultants that can occur at any section is six, the three

Orthogonal moments and three orthogonal forces. These may also be described as the

axial force F1 acting along x – axis of member, two bending moments F5 and F6 acting

about the principal y and z axes respectively of the cross section of the member, two

corresponding shear forces F3 and F2 acting along the principal z and y axes respectively

and lastly the torsion moment F4 acting about x – axis of member. The stress resultants at

any point of centroidal axis of member are shown in Fig. 3.1 and can be represented as

follows.

Fig:3.1 Six internal forces at a section of member under general loading

Fig 3.2 Various biactions at a section on an element

Numbering system is convenient for matrix notation and use of electronic computer.

Each of these actions consists essentially of a pair of opposed actions which causes

deformation of an elemental length of a member. The pair of torsion moments cause twist

of the element, pair of bending moments cause bending of the element in corresponding

plane, the pair of axial loads cause axial deformation in longitudinal direction and the

pair of shearing forces cause shearing strains in the corresponding planes. The pairs of

biactions are shown in Fig.3.2.

Primary and secondary internal forces.

In many frames some of six internal actions contribute greatly to the elastic strain energy

and hence to the distortion of elements while others contribute negligible amount. The

material is assumed linearly elastic obeying Hooke’s law. In direct force structures axial

force is primary force, shears and bending moments are secondary. Axial force structures

do not have torsional resistance. The rigid jointed plane grid under normal loading has

bending moments and torsion moments as primary actions and axial forces and shears are

treated secondary.

In case of plane frame subjected to in plane loading only bending moment is primary

action, axial force and shear force are secondary. In curved members bending moment,

torsion and thrust (axial force) are primary while shear is secondary. In these particular

cases many a times secondary effects are not considered as it is unnecessary to

complicate the analysis by adopting general method.

4 TYPES OF STRUCTURAL LOADS

For the analysis of structures various loads to be considered are: dead load, live load,

snow load, rain load, wind load, impact load, vibration load, water current, centrifugal

force, longitudinal forces, lateral forces, buoyancy force, earth or soil pressure,

hydrostatic pressure, earthquake forces, thermal forces, erection forces, straining forces

etc. How to consider these loads is described in loading standards of various structures.

These loads are idealized for the purpose of analysis as follows.

-4-

Concentrated loads: They are applied over a small area and are idealized as point loads.

Line loads: They are distributed along narrow strip of structure such as the wall load or

the self weight of member. Neglecting width, load is considered as line load acting along

axis of member.

Surface loads: They are distributed over an area. Loads may be static or dynamic,

stationary or moving. Mathematically we have point loads and concentrated moments.

We have distributed forces and moments, we have straining and temperature variation

forces.

5 DETERMINATE AND INDETERMINATE STRUCTURAL SYSTEMS

If skeletal structure is subjected to gradually increasing loads, without distorting the

initial geometry of structure, that is, causing small displacements, the structure is said to

be stable. Dynamic loads and buckling or instability of structural system are not

considered here. If for the stable structure it is possible to find the internal forces in all

the members constituting the structure and supporting reactions at all the supports

provided from statical equations of equilibrium only, the structure is said to be

determinate. If it is possible to determine all the support reactions from equations of

equilibrium alone the structure is said to be externally determinate else externally

indeterminate. If structure is externally determinate but it is not possible to determine all

internal forces then structure is said to be internally indeterminate. Therefore a structural

system may be:

(1) Externally indeterminate but internally determinate

(2) Externally determinate but internally indeterminate

(3) Externally and internally indeterminate

(4) Externally and internally determinate

These systems are shown in figures 5.1 to 5.4.

A system which is externally and internally determinate is said to be determinate system.

A system which is externally or internally or externally and internally indeterminate is

said to be indeterminate system.

Let: v = Total number of unknown internal and support reactions

s = Total number of independent statical equations of equilibrium.