Design an isolated footing for a square column, 400 mm x 400 mm

Design an isolated footing for a square column, 400 mm x 400 mm with 12-20 mm diameter longitudinal bars carrying service loads of 1500 kN with M 20 and Fe 415. The safe bearing capacity of soil is 250 kN/m2 at a depth of 1 m below the ground level. Use M 20 and Fe 415.

Step 1: Size of the footing

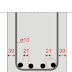
Given P = 1500 kN, qc = 250 kN/m2 at a depth of 1 m below the ground level. Assuming the weight of the footing and backfill as 10 per cent of the load, the base area required = 1500(1.1)/250 = 6.6 m2. Provide 2.6 m x 2.6 m, area = 6.76 m2 (Fig.11.29.2b).

Step 2: Thickness of footing slab based on one-way shear

Factored soil pressure = 1500(1.5)/(2.6)(2.6) = 0.3328 N/mm2, say, 0.333 N/mm2.

Assuming p = 0.25% in the footing slab, for M 20 concrete cτ = 0.36 N/mm2 (Table 19 of IS 456). 

Vu = 0.36(2600)d and Vu (actual) = 0.333(2600)(1100 - d). From the condition that Vu should be more than or equal to the actual Vu, we have (see Fig.11.29.2a, sec.11):

0.36(2600)d ≥ 0.333(2600) (1100 – d)

So, d 528.57 mm. ≥

Provide d = 536 mm. The total depth becomes 536 + 50 + 16 + 8 (with 50 mm cover and diameter of reinforcing bars = 16 mm) = 610 mm.

Step 3: Checking for two-way shear

The critical section is at a distance of d/2 from the periphery of the column. The factored shear force (Fig.11.29.2b, sec. 2222) = 0.333{(2600)2 – (400 + d)2}(10)-3 = 1959.34 kN. Shear resistance is calculated with the shear strength = ks cτ = ks(0.25) (fck)1/2; where ks = 0.5 + cβ (cl. 31.6.3 of IS 456). Here cβ = 1.0, ks = 1.5 >/ 1; so ks = 1.0. This gives shear strength of concrete = 0.25 (fck)1/2 = 1.118 N/mm2. So, the shear resistance = (1.118) 4 (936)(536) = 2243.58 kN > 1959.34 kN. Hence, ok.

Thus, the depth of the footing is governed by one-way shear.

Step 4: Gross bearing capacity

Assuming unit weights of concrete and soil as 24 kN/m3 and 20 kN/m3, respectively:

Given, the service load = 1500 kN

Weight of the footing = 2.6(2.6)(0.61)(24) = 98.967 kN

Weight of soil = 2.6(2.6)(1.0-0.61)(20) = 52.728 kN (Assuming the depth of the footing as 1.0 m).

Total = 1635.2 kN

Gross bearing pressure = 1635.2/(2.6)(2.6) = 241.893 kN/m2 < 250 kN/m2. Hence, ok.

Step 5: Bending moment

The critical section (Fig.11.29.2b, sec.3.3), is at the face of the column.

Mu = 0.333(2600)(1100)(550) Nmm = 523.809 kNm

Moment of resistance of the footing = Rbd2 where R = 2.76 (Table 3.3 of Lesson 5).

Moment of resistance = 2.76(2600)(536)(536) = 2061.636 kNm > 523.809 kNm.

Area of steel shall be determined from Eq.3.23 of Lesson 5, which is:

Mu = 0.87 fy Ast d {1 – (Ast fy/fck bd)} …. (3.23)

Substituting Mu = 523.809 kNm, fy = 415 N/mm2, fck = 20 N/mm2, d = 536 mm, b = 2600 mm, we have:

А^2 st- 67161.44578 A2stAst + 181.7861758 (105) = 6

Solving, we get Ast = 2825.5805 mm2.

Alternatively, we can use Table 2 of SP-16 to get the Ast as explained below:

Mu/bd2 = 523.809(106)/(2600)(536)(536) = 0.7013 N/mm2. Table 2 of SP-16 gives p = 0.2034.

Ast = 0.2034(2600)(536)/100 = 2834.58 mm2.

This area is close to the other value = 2825.5805 mm2.

However, one-way shear has been checked assuming p = 0.25%. So, use p = 0.25%. Accordingly, Ast = 0.0025(2600)(536) = 3484 mm2.

Provide 18 bars of 16 mm diameter (= 3619 mm2) both ways. 

The spacing of bars = {2600 – 2(50) – 16}/17 = 146.117 mm. The spacing is 140 mm c/c (Fig.11.29.2).

The bending moment in the other direction is also the same as it is a square footing. The effective depth, however, is 16 mm more than 536 mm. But, the area of steel is not needed to be determined with d = 552 mm as we are providing 0.25 per cent reinforcement based on one-way shear checking.

Step 6: Development length

Ld = fs φ/4(bdτ) = 0.87(415)(16)/4(1.6)(1.2) = 47(16) = 752 mm (cl.26.2.1 of IS 456).

Length available = 1100 – 50 = 1050 mm > 752 mm.

Step 7: Transfer of force at the base of the column

Pu = 1500(1.5) = 2250 kN

Compressive bearing resistance = 0.45 fck(A1/A2)1/2. For the column face A1/A2 = 1 and for the other face A1/A2 > 2 but should be taken as 2. In any case, the column face governs.

Force transferred to the base through column at the interface = 0.45(20)(400)(400) = 1440 kN < 2250 kN. The balance force 2250 – 1440 = 810 kN has to be transferred by the longitudinal reinforcements, dowels or mechanical connectors. As it is convenient, we propose to continue the longitudinal bars (12-20 mm diameter) into the footing. The required development length of 12-20 mm diameter bars, assuming a stress level of 0.87fy(810/2250) = 129.978 N/mm2, is 129.978(20)/4(1.6)(1.2)(1.25) = 270.8 mm. Here bdτ for M 20 = 1.2 N/mm2, increased factor of 1.6 is due to deformed bars and increased factor of 1.25 is for the compression.

Length available = 610 – 50 – 16 – 16 – 16 = 512 mm > 270.8 mm (Fig.11.29.2a). Hence, o.k. The arrangement is shown in Fig.11.29.2c.

Alternatively: Design of dowels

For the balance force 810 kN, the area of dowels = 810000/0.67(415) = 2913.15 mm2. Minimum area = 0.5(400)(400)/100 = 800 mm2 < 2913.15 mm2 (cl.34.4.3 of IS 456). Therefore, number of 16 mm dowels = 2913.15/201 = 15. The development length of 16 mm dowels in compression = 0.87(415)(16)/4(1.6)(1.2)(1.25) = 601.76 mm. Available vertical embedment length = 610 – 50 – 16 – 16 – 16 = 512 mm. So, the dowels will be extended by another 100 mm horizontally, as shown in Fig.11.29.2c.