1. Introduction
1.1 Course Outline
Goals
The goal is that you will:
1. Have fundamental knowledge of fluids:
a. compressible and incompressible;
b. their properties, basic dimensions and units;
2. Know the fundamental laws of mechanics as applied to fluids.
3. Understand the limitations of theoretical analysis and the determination of correction factors, friction factors, etc from experiments.
4. Be capable of applying the relevant theory to solve problems.
Syllabus
Basics:
• Definition of a fluid: concept of ideal and real fluids, both compressible and incompressible.
• Properties of fluids and their variation with temperature and pressure and the dimensions of these properties.
Hydrostatics:
• The variation of pressure with depth of liquid.
• The measurement of pressure and forces on immersed surfaces.
Hydrodynamics:
• Description of various types of fluid flow; laminar and turbulent flow; Reynolds’s number, critical Reynolds’s number for pipe flow.
• Conservation of energy and Bernoulli’s theorem. Simple applications of the continuity and momentum equations.
• Flow measurement e.g. Venturi meter, orifice plate, Pitot tube, notches and weirs.
• Hagen-Poiseuille equation: its use and application.
• Concept of major and minor losses in pipe flow, shear stress, friction factor, and friction head loss in pipe flow.
• Darcy-Weisbach equation, hydraulic gradient and total energy lines. Series and parallel pipe flow.
• Flow under varying head.
• Chezy equation (theoretical and empirical) for flow in an open channel.
• Practical application of fluid mechanics in civil engineering.
1.2 Programme
Lectures
There are 4 hours of lectures per week. One of these will be considered as a tutorial class – to be confirmed.
The lectures are:
• Monday, 11:00-12:00, Rm. 209 and 17:00-18:00, Rm 134;
• Wednesday, to be confirmed.
Assessment
The marks awarded for this subject are assigned as follows:
• 80% for end-of-semester examination;
• 20% for laboratory work and reports.
1.3 Reading Material
Lecture Notes
The notes that you will take in class will cover the basic outline of the necessary
ideas. It will be essential to do some extra reading for this subject.
Obviously, only topics covered in the notes will be examined. However, it often aids
understanding to hear/read different ways of explaining the same topic.
Books
Books on Fluid Mechanics are kept in Section 532 of the library. However, any of these books should help you understand fluid mechanics:
• Douglas, J.F., Swaffield, J.A., Gasiorek, J.M. and Jack, L.B. (2005), Fluid Mechanics, 5th Edn., Prentice-Hall.
• Massey, B. and Ward-Smith, J. (2005), Mechanics of Fluids, 8th Edn., Routledge.
• Chadwick, A., Morfett, J. and Borthwick, M. (2004), Hydraulics in Civil and Environmental Engineering, 4th Edn., E & FN Spon.
• Douglas, J.F. and Mathews, R.D. (1996), Solving Problems in Fluid Mechanics, Vols. I and II, 3rd Edn., Longman.
The Web
There are many sites that can help you with this subject. In particular, there are
pictures and movies that will aid your understanding of the physical processes behind
the theories.
If you find a good site, please let me know and we will develop a list for the class.
1.4 Fluid Mechanics in Civil/Structural Engineering
Every civil/structural engineering graduate needs to have a thorough understanding of fluids. This is more obvious for civil engineers but is equally valid for structural
engineers:
• Drainage for developments;
• Attenuation of surface water for city-centre sites;
• Sea and river (flood) defences;
• Water distribution/sewerage (sanitation) networks;
• Hydraulic design of water/sewage treatment works;
• Dams;
• Irrigation;
• Pumps and Turbines;
• Water retaining structures.
• Flow of air in/around buildings;
• Bridge piers in rivers;
• Ground-water flow.
As these mostly involve water, we will mostly examine fluid mechanics with this in mind.
Remember: it is estimated that drainage and sewage systems – as designed by civil
engineers – have saved more lives than all of medical science. Fluid mechanics is
integral to our work.
2. Introduction to Fluids
2.1 Background and Definition
Background
• There are three states of matter: solids, liquids, and gases.
• Both liquids and gases are classified as fluids.
• Fluids do not resist a change in shape. Therefore fluids assume the shape of the container they occupy.
• Liquids may be considered to have a fixed volume and therefore can have a free surface. Liquids are almost incompressible.
• Conversely, gases are easily compressed and will expand to fill a container they occupy.
• We will usually be interested in liquids, either at rest or in motion.
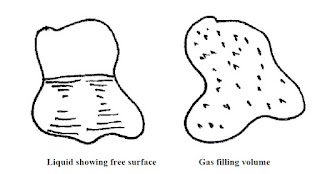 |
| The behaviour of fluids in containers |
Definition
The strict definition of a fluid is:
A fluid is a substance which conforms continuously under the action of
shearing forces.
To understand this, remind ourselves of what a shear force is:
 |
| Application and effect of shear force on a book |
Definition Applied to Static Fluids
Definition Applied to Fluids in Motion
 |
| Definition Applied to Fluids in Motion |
 |
| Ideal fluid |
 |
| Fluid Mechanics |
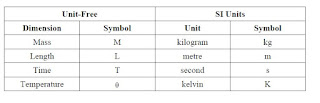 |
| Système International |
Derived Units
 |
| SI Unit |
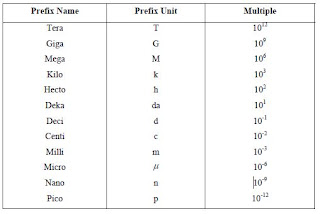 |
| SI Prefixes |
2.3 Properties
Relative Density (Specific Gravity)
Bulk Modulus
In analogy with solids, the bulk modulus is the modulus of elasticity for a fluid. It is the ratio of the change in unit pressure to the corresponding volume change per unit volume, expressed as:
(Change in Volume/Original Volume) = (Change in pressure/Bulk Modulus)
In which the negative sign indicates that the volume reduces as the pressure
increases. The bulk modulus changes with the pressure and density of the fluid, but
for liquids can be considered constant for normal usage. Typical values are:
• Water: 2.05 GN/m3;
• Oil: 1.62 GN/m3.
The units are the same as those of stress or pressure.
Viscosity
The viscosity of a fluid determines the amount of resistance to shear force.
Viscosities of liquids decrease as temperature increases and are usually not affected
by pressure changes. From Newton’s Law of Viscosity:




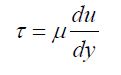






No comments:
Post a Comment
If you are getting more information from civilengineerfriend page please give your comments. Share the page information in your whatsapp group. Subscribe our page to get more information.