Draw the layout for five common methods of on street parking and describe each

On street parking

On street parking means the vehicles are parked on the sides of the street itself. This will be usually controlled by government agencies itself. Common types of on-street parking are as listed below. This classification is based on the angle in which the vehicles are parked with respect to the road alignment. As per IRC the standard dimensions of a car is taken as 5×2.5 metres and that for a truck is 3.75×7.5 metres.

Parallel parking: The vehicles are parked along the length of the road. Here there is no backward movement involved while parking or unparking the vehicle. Hence, it is the most safest parking from the accident perspective. However, it consumes the maximum curb length and therefore only a minimum number of vehicles can be parked for a given kerb length. This method of parking produces least obstruction to the on-going traffic on the road since least road width is used. Parallel parking of cars is shown in figure 1.

Parallel parking

The length available to park  number of vehicles, L = 

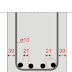
30° parking: In thirty degree parking, the vehicles are parked at 30° with respect to the road alignment. In this case, more vehicles can be parked compared to parallel parking. Also there is better maneuverability. Delay caused to the traffic is also minimum in this type of parking. An example is shown in figure 2. From the figure,

For N vehicles, L = AC + (N-1)CE =5.58+(N-1)5 =0.58+5N

30° parking 

45°parking: As the angle of parking increases, more number of vehicles can be parked. Hence compared to parallel parking and thirty degree parking, more number of vehicles can be accommodated in this type of parking. From figure 3, length of parking space available for parking N number of vehicles in a given kerb is L= 3.54 N+1.77  

45°parking60° parking: The vehicles are parked at 60° to the direction of road. More number of vehicles can be accommodated in this parking type. From the figure 4, length available for parking N vehicles =2.89N+2.16.

60° parking

Right angle parking: In right angle parking or 90°parking, the vehicles are parked perpendicular to the direction of the road. Although it consumes maximum width kerb length required is very little. In this type of parking, the vehicles need complex maneuvering and this may cause severe accidents. This arrangement causes obstruction to the road traffic particularly if the road width is less. However, it can accommodate maximum number of vehicles for a given kerb length. An example is shown in figure 5. Length available for parking N number of vehicles is L = 2.5N.

Right angle parking